Weekly Reading3 – Ageing threatens sustainability of smallholder farming in China

My advisor recommended this paper to me. He asked me to understand this article and grasp the methods it employs. After all, this article was published in Nature, a journal that I will probably only ever admire from a distance in my lifetime.

Cite this article: Ren, C., Zhou, X., Wang, C. et al. Ageing threatens sustainability of smallholder farming in China. Nature 616, 96–103 (2023). https://doi.org/10.1038/s41586-023-05738-w

Overview

Research Questions: How does aging affect sustainable agricultural development? What measures should be taken to mitigate the effects of ageing?

Research approach:

1. Multiple regression model (MRM) is used to test the relationship between rural population ageing (the proportion of individuals over 65 years old at the household level) and agricultural sustainability.
2. Structural equation model (SEM) is introduced to show both the direct and the indirect influencing pathways.
3. Compare the performance differences between traditional smallholder farmers and new agricultural models (cooperatives, large-scale farms).
4. Forecasting changes in agricultural sustainability indicators under different policy interventions (e.g., promotion of new models) (to 2100)

Aging is bad

Descriptive analysis:

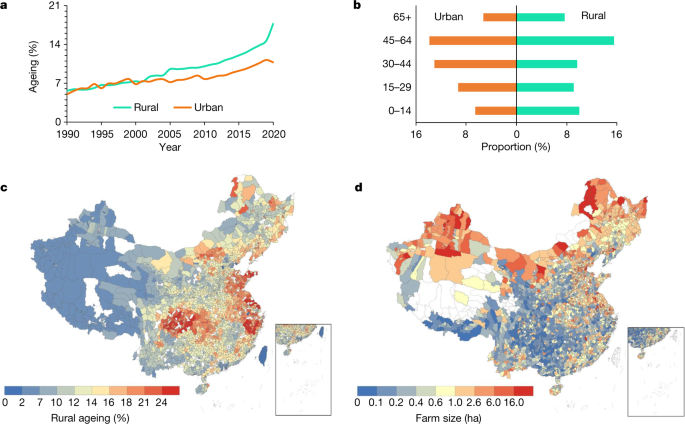
Authors used two maps show the level of aging and farm size at the county level, and visually show that farms in heavily aging areas tend to be smaller. (BTW, I think using a map can be a good way to show your results under certain conditions, but many people worry it might pose potential political risks.)

MRM analysis:

Y: Agricultural sustainability: Total agricultural input, output, labor productivity, fertilizer input, manure, fertilizer loss, farmer’s income, farm size and machine input.

X: Ageing (the proportion of people ≥65 years old in rural households), Education (average years of education of family members aged 15 and over), Farm size (logarithm of total cultivated area covering all crops)

Control variables: Adult (the adult farmers ratio), Income ratio (income ratio from non-agricultural sectors), Crop type, Plot number, county and year effect

Result: Ageing is correlated with a decrease in agricultural inputs, with a 0.3% reduction in total inputs for each percentage point increase in the ageing ratio ceteris paribus, mainly concerning chemical fertilizers and manure, and machinery and technology adoption. Consequently, a 0.33% and 0.14% decline in agricultural output and yield per area, respectively, was related to each percentage point increase in the ageing ratio ceteris paribus, leading to the decline of labor productivity. (Table 1 and Supplementary Table 1)

Tobit regression model:

Variables of transferred-out and -in cropland, abandoned cropland, machine and manure input contain a fraction of the variables with values of 0, but are continuously distributed at positive values.

For those values, the Tobit model was employed for validation, and results similar to those of the MRN were obtained.

Counterfactual analysis：

Assuming that the level of aging is still above 1990 levels, the authors use a very simple method to estimate the level of agricultural development that should occur in 2019 under such a scenario.

First, authors calculated the differences of explained variables of agricultural sustainability due to ageing changes (AG) between 2019 and 1990. In this model (eq2), the independent variable is the difference in aging degree and the difference in adult ratio between 2019 and 1990, and the dependent variable is the difference in agricultural sustainability indicators between the two years.

$$ \begin{multline} \text{Agriculture}_{it} = \alpha + \beta \times \text{Ageing}_{it} + \gamma \times \text{Education}_{it} \\ + \delta \times \text{Farm_size}_{it} + \theta_{1} \times \text{Adult}_{it} + \theta_{2} \times \text{Income_ratio}_{it} \\ + \theta_{3} \times \text{Crop_type}_{it} + \theta_{4} \times \text{Plot_number}_{it} + \varphi_{t} + \mu_{it} \tag{1} \end{multline} $$

$$ \Delta \ln Y_{ij}^{AG} = \beta_j \times \Delta \text{Ageing}_{ij} + \theta_{1j} \times \Delta \text{Adult}_{ij}\tag{2} $$

I looked at the equation for a while wondering why it had a solution, but I finally realized that the beta and θ here use the coefficient results from the previous full formula using all 2019 data (eq1). That is, assuming that all other things being equal, changing only the size of these two x’s has an effect on y.

The so-called counterfactual analysis is what would happen to y if we replaced the aging and adult population in 2019 with 1990 numbers. This is a good idea.

Why aging is bad

According to the symbols of the coefficients in the previous MRM regression, the authors propose several influence paths:

1. ageing → lower education → less scientific, state-of-the-art methods
2. ageing → smaller farm size → more abandoned or transferred croplands
3. ageing → decrease in agricultural inputs → decline of labor productivity

SEM analysis:

A friend of mine said that she didn’t expect SEM to appear in such a journal, and she was under the impression that it was a very low method. I don’t know much about SEM, but the articles I read are usually used to analyze the results of questionnaire questions. Among researchers at my level, questionnaire research itself is difficult to be scientific and reasonable, so I fully understand her point of view. But that doesn’t mean there’s anything wrong with this approach.

What can we do to avoid this badness

New agricultural farming models have been encouraged by the Chinese government and increasingly emerging since the 2010s, mainly including family, cooperative and industrial farming, to transform the smallholder-dominated status quo and improve overall agricultural performance.

The authors believe that new agricultural models can effectively mitigate the effects of aging. First, the two-sample T-test showed that the new agricultural model was significantly better than the traditional agriculture on related indicators (aging, farm size, etc.)

Predictive analysis by SSPs

Shared Socioeconomic Pathways (SSPs) are a set of scenarios developed by the climate research community to explore how global society, demographics, and economics might evolve over the 21st century. They are used alongside Representative Concentration Pathways (RCPs), which describe different levels of greenhouse gas emissions, to analyze the interactions between socioeconomic development and climate change.

The authors based analysis of future socioeconomic development on the SSP scenarios to determine the impact of population ageing on agricultural sustainability. Data on aging, percentage of adult farmers, and education at the household level are derived for 2020-2100. Assuming that other variables remain at the 2019 level, the predicted values of agricultural sustainability indicators in the context of future aging and education are calculated.

The results show that under different SSP scenarios, the indicators of future agricultural sustainability predicted by the introduction of new agricultural forms are significantly better than those without the introduction of new agricultural forms. This suggests that The decline in agricultural performance related to ageing can be reversed by promoting an increasing uptake of new farming models.

Comments

I think the best aspect of this paper is that it not only verifies the correlation between aging and threats to agricultural sustainability at present, but also conducts an in-depth analysis of how conditions would differ if aging had remained at past levels. Through SSP predictions, it explores counterfactual scenarios for the future. This validates their proposed core solution – the promising future of new agricultural models. This approach is far more concrete and reliable than proposing solutions without substantiation.

Methodologically, the intensive quantitative methods convey a wealth of information. The key methods that need to be studied include MRM, SEM, and Tobit. The author’s counterfactual analysis approach is very enlightening, helping me understand the value of the SSP database and preset scenarios.

To be honest, for someone like me with limited econometric background, it might take a month to fully understand this type of paper. There are indeed many aspects I find puzzling. Although this paper provides extensive materials, the specific implementation details and interpretations are scattered across different materials, requiring careful reading to connect the pieces together.

Supplement: Besearch methods

Multiple regression model (MRM):

A statistical technique used to examine the relationship between a single dependent variable (outcome) and two or more independent variables (predictors). It extends simple linear regression by incorporating multiple predictors, allowing for the analysis of how each variable contributes to explaining the variation in the outcome while controlling for others. The model is expressed as:

$$ Y=β_0+β_1X_1+β_2X_2+⋯+β_kX_k+ϵ $$

Y: Dependent variable. β0: Intercept (baseline value when all predictors are zero). β1, β2, …, βk: Coefficients representing the effect of each predictor X1, X2, …, Xk on Y. ϵ: Error term (unexplained variation).

Key assumptions include linearity, independence of errors, homoscedasticity (constant variance of errors), normality of errors, and no severe multicollinearity among predictors.

Applications: to predict outcomes, test hypotheses, or control for confounding factors. For example, predicting house prices based on size, location, and age while adjusting for other variables.

Structural equation model (SEM):

A statistical method to study complex relationships between variables. It is used to understand how multiple variables interact in real-world systems. It combines:

• Factor analysis: Measures hidden concepts (e.g., “customer loyalty”) using multiple observed variables (e.g., survey questions).
• Path analysis: Tests direct/indirect effects (e.g., “education → income → life satisfaction”).

Steps:

• Define Model: Draw a diagram linking variables (e.g., “Stress → Sleep Quality → Work Performance”). Include both observed data (e.g., survey scores) and hidden factors (e.g., “stress”).
• Collect Data & Run Analysis: Use software (e.g., AMOS, R’s lavaan) to test if data fits your model.
• Validate & Explain: Check fit indices (e.g., RMSEA < 0.08 = good fit). Interpret path coefficients (e.g., “Stress reduces sleep quality by 30%”).

Tobit regression model:

When the observed dependent variable (Y) has limited value ranges (such as Y can only take non-negative values or is “truncated” above or below a fixed value), but the potential true variable (Y*) may exceed this range, traditional linear regression (OLS) will produce bias. The Tobit model can correct this bias and provide more accurate parameter estimates.

Tobit can solve:

1. Data Censoring: The observed values of dependent variable Y are censored at a certain threshold (for example, in agricultural research, farmers’ “fertilizer usage” has a minimum of 0/no fertilization, but potential demand could be negative).
2. Data Truncation: During data collection, samples outside a certain range are directly excluded, resulting in missing true data, such as when studying “the impact of farm size on production efficiency,” only surveying farms ≥1 hectare while ignoring small-scale farmers.
3. Sample Selection Bias: The dependent variable is limited by certain selection mechanisms (for example, only farmers participating in specific agricultural projects can receive high subsidies, with data missing for non-participants).

Steps:

$$ \begin{equation} Y_i = \begin{cases} Y_i^* = \beta X_i + \epsilon_i & \text{if } Y_i^* > c \\ c & \text{if } Y_i^* \leq c \end{cases} \quad \text{where} \quad \epsilon_i \sim N(0, \sigma^2) \end{equation} $$

1. Confirm if Tobit model is needed: Observe if Y has a large accumulation at a certain threshold (c) (e.g., 50% of farmers’ fertilizer usage is 0); Examine OLS results, if residuals show systematic deviation near the truncation point, Tobit should be used.
2. Model specification: $Y_i^∗$ is the latent variable, following normal distribution: $ϵ_i∼N(0,σ^2)$.
3. Parameter estimation: Maximum Likelihood Estimation (MLE): MLE through joint estimation of linear component of latent variable and error term variance.
4. Result interpretation: β represents the marginal effect of X on latent variable Yi*(different from OLS). BUT, the actual observed decrease in usage needs to be calculated using the marginal effects formula.

Limitations and Alternatives:

1. Strong Distribution Assumption: Requires error terms to strictly follow normal distribution for consistent estimates. For non-normal errors: Use semi-parametric methods like CLAD (Censored Least Absolute Deviations).
2. Homoscedasticity Assumption: If heteroscedasticity exists (e.g., different error variances between large and small farms), heteroscedastic Tobit model should be used.
3. Corner Solution Issues: When Y observations cluster at specific values but theoretically could exceed them, consider using Two-Part Model (e.g., Logit+OLS).
4. Sample Selection Bias: Consider using Heckman selection model.
5. Clear Censoring Point: May not be applicable when censoring mechanism is unclear (e.g., complex missing data patterns).

Comparison of ln(x+1) MRM and Tobit models

Logarithmic transformation (ln(x+1) + MRM)

• Dependent variable is right-skewed, but with a low proportion of zero values (e.g., <20%), or zeros represent “true zeros” (such as no income).
• Explains the percentage change (elasticity) of dependent variable relative to explanatory variables.
• Data has no severe truncation, and residuals approximate normal distribution after transformation.

Tobit model:

• Dependent variable has many zero values (e.g., ≥30%), and zeros represent corner solutions, as active choices.
• Shows the absolute effect of explanatory variables on dependent variable (e.g., Y increases by β units for each unit increase in X).
• Data has potential continuous distribution (unobserved Y*).

read on 23/3/2025